Sudoku mit Dancing Links (DLX) lösen
Während die bisher vorgestellten Algorithmen alle relativ "straight forward" waren, es also recht einfach zu verstehen ist, wie und warum sie funktionieren, ist das bei "Dancing Links" anders.
Diese Technik, die sich überhaupt nicht zum lösen von Hand eignet (noch viel weniger als normales Backtracking), ist nichttrivial und daher recht ausführlich erklärt.
Es gibt viel englischsprachige Literatur zu dem Algorithmus "Dancing Links" oder DLX (Dancing Links - Algorithmus X) von Donald E. Knuth, auf deutsch etwa "Tanzende Zeiger". Hier möchte ich eine deutschsprachige Erklärung liefern.
topDie Aufgabe
Das Problem, das man mit den "Dancing Links" im Allgemeinen lösen will und kann, ist folgendes:
Man hat eine Menge A, und verschiedene Mengen B1, B2, B3,... Jetzt will man aus den B1, B2, B3, ... mehrere Bs so auswählen, dass kein Element in den Bs doppelt vorkommt, und jedes Element aus A in den Bs vorkommt.
Man nennte es das "Problem der exakten Überdeckung", oder auf Englisch "exact cover".
Zu Abstrakt, zu schnell?
topEin Beispiel
Stellen wir uns vor, auf einer Insel sitzen ein paar Menschen, mit Namen Anton, Berta, Claudia, Daniel und Eva.
Diese netten Leute formen unsere Menge A.
Sie wollen von der Insel weg, und haben dafür Boote zur Verfügung. Allerdings vertragen sich manche nicht gut, und Antont und Berta sind ein Liebespaar, die nicht getrennt werden wollen.
Sie können sich nur folgende Kombinationen vorstellen, wie sie sich auf die Boote verteilen:
top| Name der Gruppe | Mitglieder |
|---|---|
| B1 | Anton, Berta |
| B2 | Anton, Berta, Claudia |
| B3 | Anton, Berta, Daniel |
| B4 | Claudia, Eva |
| B5 | Claudia, Daniel, Eva |
Natürlich wollen sie niemanden zurücklassen, und jede Person kann nur in einem Boot gleichzeitig sein.
In diesem Fall haben sie Glück, es gibt zwei Kombinationen, wie sie sich nach ihren Vorstellungen aufteilen können: B1 und B5 oder B3 und B4.
Wenn man ein wenig durchprobiert, wird das einem sehr schnell klar. Aber was ist, wenn man hunderte oder Tausende von Elementen hat, und noch sehr viel mehr mögliche Gruppen?
Dann muss man einem Computer beibringen, wie man so ein Problem gut löst.
topVorbereitung zum Lösen
Damit ein Computer so ein Problem gut lösen kann, muss man es in eine Tabelle oder Matrix schreiben. Dazu trät man nach rechts die möglichen Personen (um bei obigen Beispiel zu bleiben) auf, und nach unten die möglichen Gruppen.
Wenn eine Person in einer Gruppe ist, schreibt man eine Eins hinein, sonst eine Null.
| Gruppe | Anton | Berta | Claudia | Daniel | Eva |
|---|---|---|---|---|---|
| B1 | 1 | 1 | 0 | 0 | 0 |
| B2 | 1 | 1 | 1 | 0 | 0 |
| B3 | 1 | 1 | 0 | 1 | 0 |
| B4 | 0 | 0 | 1 | 0 | 1 |
| B5 | 0 | 0 | 1 | 1 | 1 |
Jetzt kann man das Problem auch umformulieren: Wir wollen Zeilen aus dieser Tabelle so auswählen, dass in jeder Spalte genau eine Eins steht.
topLösungsidee
Die Lösungsidee, die Donald E. Knuth entwickelt hat, ist rekursiv, das heißt der Algorithmus verwendet sich selbst, allerdings auf ein kleineres Problem angewandt.
- Wenn die Matrix leer ist, wurde eine Lösung gefunden.
- Wenn sie nicht leer ist, wähle eine Spalte
s. - Wähle zufällig eine Zeile
z, die in der Spalteseine Eins stehen hat. Diese Zeile wird Teil der Zwischenlösung - Für jede Spalte
n, in der in der Zeilezeine 1 steht:- Lösche die Spalte
naus der Matrix - Lösche alle Zeilen, die in der gelöschten Matrix eine 1 stehen hatten.
- Lösche die Spalte
- Wiederhole die Prozedur für die übriggebliebene Matrix
Dieses Verfahren wird Algorithmus X
Schritt Nummer 1 hört sich am Anfang komisch an, ein Beispiel wird es jedoch veranschaulichen.
topUnser Beispiel mit Algorithmus X gelöst
1. Die Matrix ist nicht leer, wir haben noch keine Lösung gefunden.
2. Wähle eine Spalte. Wie man genau eine Spalte wählt wird später noch erklärt, hier wird erstmal die erste Spalte gewählt, also Anton.
3. Wähle eine Zeile, in der in der gewählten Spalte eine 1 steht. Das könnte B1, B2 oder B3 sein. Mein Zufallsgenerator sagt mir: Wähle Zeile B1. Also gehört B1 zu unserer vorläufigen Lösung.
4. Jetzt kommt das Löschen. Spalte 1 wird gelöscht, und alle Zeilen, die in der Spalte 1 eine Eins stehen haben. Genauso wird für Spalte 2 verfahren, weil in der Zeile B1
Übrig bleibt:
| Gruppe | Claudia | Daniel | Eva |
|---|---|---|---|
| B4 | 1 | 0 | 1 |
| B5 | 1 | 1 | 1 |
Die Tabelle ist ganz schön klein geworden.
Der 5. Schritt sieht das Wiederholen vor, also wiederholen wir:
1. Die Matrix ist nicht leer, wir haben keine Lösung gefunden.
2. Wähle eine Spalte. Sagen wir, Spalte 1 der übriggeblienen Matrix, also Claudia.
3. Wähle eine Zeile, die ein Spalte 1 eine 1 stehen hat. Das trifft auf beide übriggeblienen Zeilen zu, hier wird Zeile B4 gewählt.
4. Entferne die gewählte Zeile, sowie alle Spalten, in denen dort eine 1 steht, sowie alle Zeilen, die in den gelöschten Spalten eine 1 stehen haben
Damit ist die Matrix leer, der Algorithmus ist fertig mit dieser Teillösung. Allerdings ist das Überdeckungsproblem nicht gelöst, weil bisherige Lösung, die Menge aus B1 und B4, die Spalte "Daniel" nicht abdeckt.
Also muss man einen Schritt zurückgehen, und eine andere Wahl treffen (Backtracking).
In diesem Fall war die letzte Wahl die von B4, sie muss also rückgängig gemacht werden und durch die einzig verbleibende Alternative ersetzt werden, B5.
Dann ist das Problem gelöst
topDiskussion
Wenn man das Beispiel und den Algorithmus vergleicht, merkt man schon, dass die Lösungsidee nicht alle Fälle genau beschreibt.
Für eine genauere Diskussion des Algorithmus sei hier auf das Originalwerk von D. E. Knuth (Englisch, PDF) verwiesen.
Man kann jedoch noch einiges verbesserns, was die Geschwindigkeit angeht, indem man eine geeignetere Datenstruktur wählt.
topDie Implementierung als zweidimensionales Array hat zwei Probleme:
- Das Suchen nach Einsen dauert lange
- Das löschen der Zeilen und Spalten daurtert lange
Beide Probleme kann man mit doppelt verlinkten Listen (double linked lists) lösen.
topTanzende Zeiger
Um die genialen tanzenden Zeiger zu verstehen, muß man erst etwas über doppelt verlinkte Listen wissen, und wie man daraus spärlich besetzte Matrizen aufbaut.
Doppelt verlinkte Listen
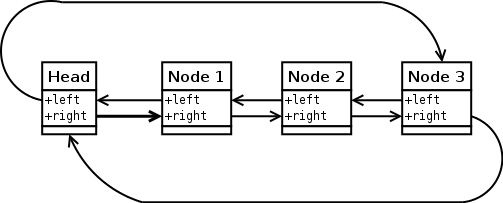
Doppelt verlinkte Listen funktioniert folgendermaßen: Für jeden Eintrag der Liste wird nicht nur der Inhalt gespeichert, sondern auch der linke und rechte Nachbar.
In Pseudocode sieht das so aus:
struct node {
int data;
node* left;
node* right;
};
Wobei eine Liste immer aus mindestens einem Element, dem Kopf der
Liste, besteht. Wenn die Liste keine Daten enthält zeigen
left und right auf den Kopf selbst.
 top
top
Wenn man ein Zeiger auf ein Element node1 hat, und
dieses löschen will, so reicht es, zwei Zeiger neu zuzuweisen
("verbiegen"):
node->left->right = node->right; node->right->left = node->left;

Damit zeigt node1 zwar immer noch auf seine Nachbarn,
aber wenn sich man vom Kopf der Liste ausgehend an den Zeigern entlang
hangelt, kommt man nicht mehr dort hin. Es ist also effektiv
gelöscht.

In den Grafiken sind die Daten weggelassen, die in den einzelnen Elementen gespeichert sein können, da sie auf das verbiegen der Zeiger keinen Einfluss haben.
Übrigens kann ein gelöschtes Element sehr einfach wieder hergestellt werden, weil es immer noch Zeiger nach rechts und links besitzt. Dazu reicht
node1->left->right = node1; node1->right->left = node1;
Hier gibt es eine genauere Beschreibung der doppelt verketteten Liste.
topSpärlich besetzte Matrizen
Wenn eine Matrix nur wenig Element hat, wie das bei den hier diskutierten Problemen häufig der Fall ist, lohnt es sich, die Matrix aus doppelt verlinkten Listen aufzubauen.
Und zwar verlinkt man die Elemente doppelt nach horizontal und Vertikal, wie in folgender Grafik zu sehen ist:

(Klicken Sie auf das Bild, um eine größere Version zu sehen).
Dabei ist nicht jeder Link einzeln dargestellt, da überall, wo es einen Zeiger in eine Richtung gibt, auch ein Zeiger in die Rückrichtung gibt.
Diese Datenstruktur erlaubt es, schnell die nicht-leeren Einträge zu finden, da nur nicht-leere Einträge (in unserem Beispiel Einsen) darin vorkommen.
Der zweite große Vorteil für unseren Algorithmus ist, dass man Zeilen und Spalten sehr schnell und einfach löschen kann.
Hier der Beispielcode zum Löschen einer Zeile
// Die Struktur sieht so aus:
struct node {
node* left,
node* right,
node* top,
node* bottom
}
// Lösche Zeile eine Zeile, wenn z der Zeiger zum Kopf der
// Zeile ist:
for (node i = z->right; i != z; i = i->right){
i->top->bottom = i->bottom;
i->bottom->top = i->top;
}
z->top->bottom = z->bottom;
z->bottom->top = z->top;
Wenn man diese Datenstruktur für den oben beschriebenen Algorithmus X verwendet, besteht ein sehr großer Teil des Programms daraus, sich an Zeigern entlangzuhangeln und sie "umzubiegen". Daher der Name "Dancing Links" oder auf Deutsch "Tanzende Zeiger".
topSudokus mit "Dancing Links" lösen
Man kann Sudoku als "exact cover"-Problem auffassen, und damit mit "Dancing Links" lösen.
Zunächst muß man sich überlegen, was die Bs sind:
In jede Zelle kann entweder genau eine Zahl 1, 2, 3, ... 9 hinein.
Deswegen ist z.B. B1: "In Zelle (1, 1) kommt Zahl 1 hinein", B2 wäre "In Zelle (1, 1) kommt Zahl 2 hinein", usw., bis hin zu B729: In Zelle (9, 9) kommt Zahl 9 hinein".
Wir haben also 9*9*9 = 729 Mengen, aus denen wir wählen können.
Jetzt muss man nur noch die Sudokuregeln so umformulieren, dass sie ein Überdeckungsproblem darstellen:
- In jede Zeile muss jede Zahl einmal hinein (9*9 Bedingungen)
- In jede Spalte muss jede Zahl einmal hinein (9*9 Bedingungen)
- In jeden Block muss jede Zahl einmal hinein (9*9 Bedingungen)
- In jeder Zelle darf jede Zahl nur einmal stehen (9*9 Bedingungen)
Das sind also 9*9*4 = 324 Bedingungen.
Die Matrix des Überdeckungsproblems hat also die Abmessungen 324x729, hat also 236.196 Einträge, von denen die meisten Null sind.
Man kann sich leicht überlegen, dass in jeder Zeile vier Einsen stehen müßen, da jede Zahl in je einer Spalte, Zeile und einem Block vorkommt sowie eine Zelle füllt, die Matrix hat also 729*4 = 2916 nicht verschwindende Einträge, das ist jeder einundachzigste.
In verschiedenen Programmiererforen wird berichtet, dass die Methode der tanzenden Zeiger eine sehr schnelle Methode zum lösen von Sudokus ist, schneller als logikbasierte Solver, die im Zweifelsfall Backtracking verwenden.
topReferenzen
- Wikipedia-Eintrag zu Dancing Links, Englisch
- Originalwerk von Donald E.Knuth, pdf, Englisch
- Ergebnisse eines Programmierwettbewerbs mit Thema Sudoku